图灵奖得主姚期智领衔的首篇大语言模型论文来了！一出手，瞄准的就是“让大模型像人一样思考”这个方向——不仅要让大模型一步步推理，还要让它们学会“步步为营”，记住推理中间的所有正确过程。

具体来说，这篇新论文提出了一种叫做累积推理（Cumulative Reasoning）的新方法，显著提高了大模型搞复杂推理的能力。

要知道，大模型基于思维链等，可以进行问题推理，但面对“要拐好几个弯”的问题，还是容易出错。

累积推理正是在此基础上，加入了一个“验证者”，及时判断对错。由此模型的思考框架也从链状和树状，变成了更复杂的“有向无环图”。

这样一来，大模型不仅解题思路更清晰，还生出了一手“玩牌”的技巧：

在代数和几何数论等数学难题上，大模型的相对准确率提升了42%；玩24点，成功率更是飙升到98%。

从这个角度出发设计的累积推理，效果比思维链（CoT）和思维树（ToT）更好。

那么，这种新方法究竟长啥样？我们一起展开看看。

突破思维链&树“瓶颈”

累积推理的核心，在于改进了大模型思维过程的“形状”。

具体来说，这个方法用到了3个大语言模型：

·提议者 (Proposer)：不断提出新命题，即基于当前思维上下文，建议下一步是什么。

·验证者 (Verifier)：核查提议者的命题准确性，如果正确就将它添加到思维上下文中。

·报告者 (Reporter)：判断是否已经能得到最终解决方案，来确定是否结束推理过程。

推理过程中，“提议者”先给出提案，“验证者”负责评估，“报告者”决定是否要敲定答案、终止思考过程。

有点像是团队项目里的三类角色：小组成员先头脑风暴出各种idea，指导老师“把关”看哪个idea可行，组长决策什么时候完成项目。

所以，这种方法究竟是怎么改变大模型思维“形状”的？

要想理解这一点，还得先从大模型思维加强方法“鼻祖”思维链（Chain of Thought,CoT）说起。

这个方法在2022年1月由OpenAI科学家Jason Wei等人提出，核心在于给数据集中的输入加一段“逐步推理”文字，激发出大模型的思考能力。

基于思维链原理，谷歌也快速跟进了一个“思维链PLUS版”，即CoT-SC，主要是进行多次思维链过程，并对答案进行多数投票（majority vote）选出最佳答案，进一步提升推理准确率。

但无论思维链还是CoT-SC，都忽略了一个问题：题目不止有一种解法，人类做题更是如此。

因此，随后又出现了一种名叫思维树（Tree of Thought,ToT）的新研究。

这是一种树状检索方案，允许模型尝试多种不同的推理思路，并自我评估、选择下一步行动方案，必要时也可以回溯选择。

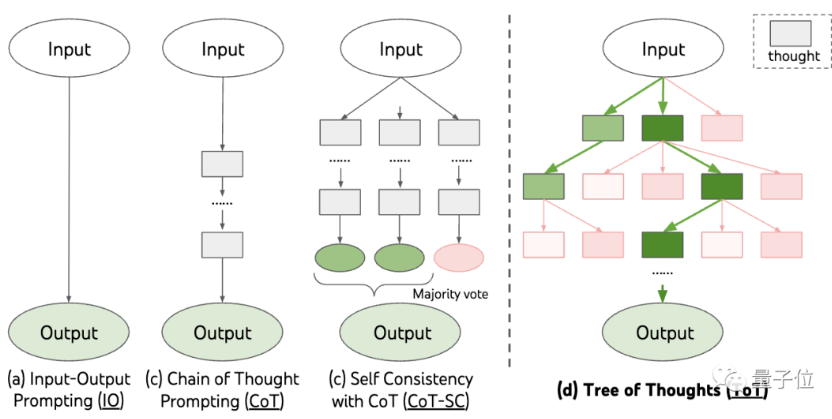
从方法中可以看出，思维树比思维链更进一步，让大模型思维“更活跃”了。

这也是为什么玩24点时，思维链加成的GPT-4成功率只有4%，但思维树成功率却飙升到74%。

BUT无论思维链、CoT-SC还是思维树，都有一个共同的局限性：

它们都没有设置思维过程中间结果的储存位置。

毕竟不是所有的思维过程都能做成链或者树，人类想东西的方式往往还要更复杂。

这次的累积推理新框架，在设计上就突破了这一点——

大模型的整体思维过程不一定是链或树，还可以是一个有向无环图（DAG）！（嗯，有神经突触内味了

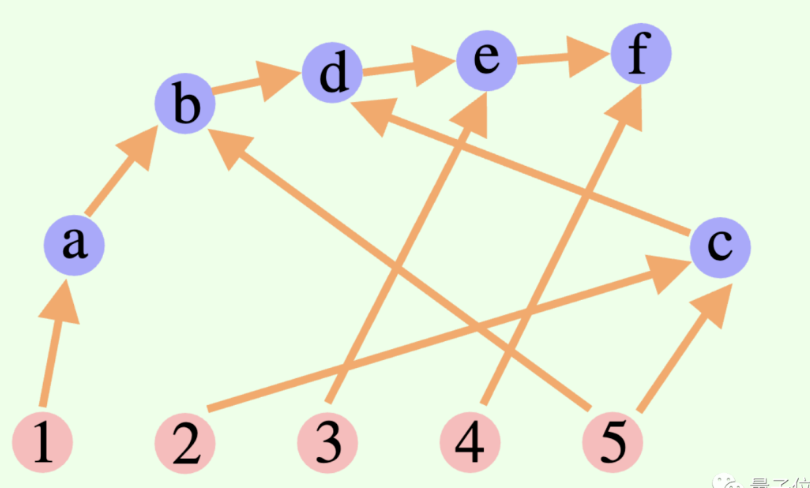
△图中的边都有方向，并且不存在任何循环路径；每个有向边是一个推导步骤

这也就意味着，它可以将所有历史上正确的推理结果存储于内存中，以便在当前搜索分支中探索。（相比之下，思维树并不会存储来自其它分支的信息）

但累积推理也能和思维链无缝切换——只要将“验证者”去掉，就是一个标准的思维链模式。

基于这种方法设计的累积推理，在各种方法上都取得了不错的效果。

做数学和搞逻辑推理都在行

研究人员选择了FOLIO wiki和AutoTNLI、24点游戏、MATH数据集，来对累积推理进行“测试”。

提议者、验证者、报告者在每次实验中使用相同的大语言模型，用不同的prompt来设定角色。

这里用作实验的有GPT-3.5-turbo、GPT-4、LLaMA-13B、LLaMA-65B这些基础模型。

值得一提的是，理想情况下应该使用相关推导任务数据专门预训练模型、“验证者”也应加入正规的数学证明器、命题逻辑求解器模块等。

1、逻辑推理能力

FOLIO是一阶逻辑推理数据集，问题的标签可以是“true”、“False”、“Unknown”；AutoTNLI是高阶逻辑推理数据集。

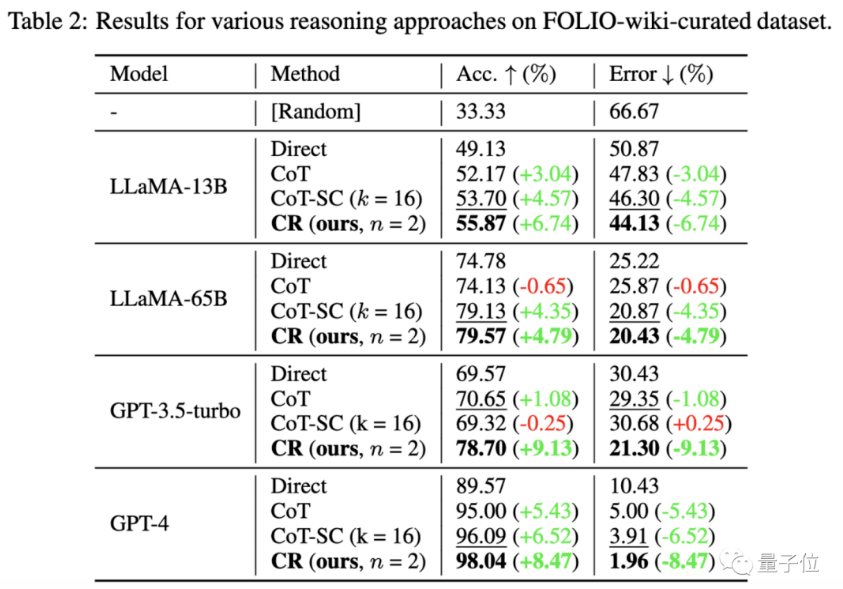
在FOLIO wiki数据集上，与直接输出结果（Direct）、思维链（CoT）、进阶版思维链（CoT-SC）方法相比，累积推理（CR）表现总是最优。

在删除数据集中有问题的实例（比如答案不正确）后，使用CR方法的GPT-4推理准确率达到了98.04%，并且有最小1.96%的错误率。

再来看AutoTNLI数据集上的表现：

与CoT方法相比，CR显著提高了LLaMA-13B、LLaMA-65B的性能。

在LLaMA-65B模型上，CR相较于CoT的改进达到了9.3%。

2、玩24点游戏能力

ToT最初论文中用到的是24点游戏，所以这里研究人员就用此数据集来做CR和ToT的比较。

ToT使用固定宽度和深度的搜索树，CR允许大模型自主确定搜索深度。

研究人员在实验中发现，在24点的上下文中，CR算法和ToT算法非常相似。不同点在于，CR中算法每次迭代最多产生一个新的状态，而ToT在每次迭代中会产生许多候选状态，并过滤、保留一部分状态。

通俗来讲，ToT没有上面提到的CR有的“验证者”，不能判断状态（a、b、c）正误，因此ToT比CR会探索更多无效状态。

最终CR方法的正确率甚至能达到98%（ToT为74%），且平均访问状态数量要比ToT少很多。

也就是说CR不仅有更高的搜索正确率，也有更高的搜索效率。

3、数学能力

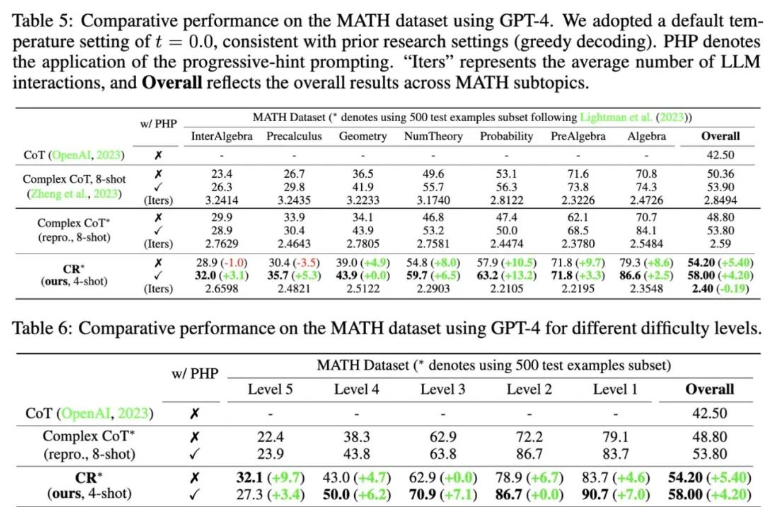
MATH数据集包含了大量数学推理题目，包含代数、几何、数论等，题目难度分为五级。

用CR方法，模型可以将题目分步骤拆解成能较好完成的子问题，自问自答，直到产生答案。

实验结果表明，CR在两种不同的实验设定下，正确率均超出当前已有方法，总体正确率可达58%，并在Level 5的难题中实现了42%的相对准确率提升，拿下了GPT-4模型下的新SOTA。